In the previous article, we saw defining ordering of blocks and transactions in a DAG topology can be a challenge. In this article, we describe Taraxa’s mechanism for ensuring not just ordering, but secure and fair ordering in a block DAG.
Why Ordering is Challenging
What’s hard about ordering in a block DAG?
Just by looking at any DAG data structure, we can only establish partial ordering, which means we can only be certain about the ordering relationships between certain blocks, but not all blocks. Here’s an example.
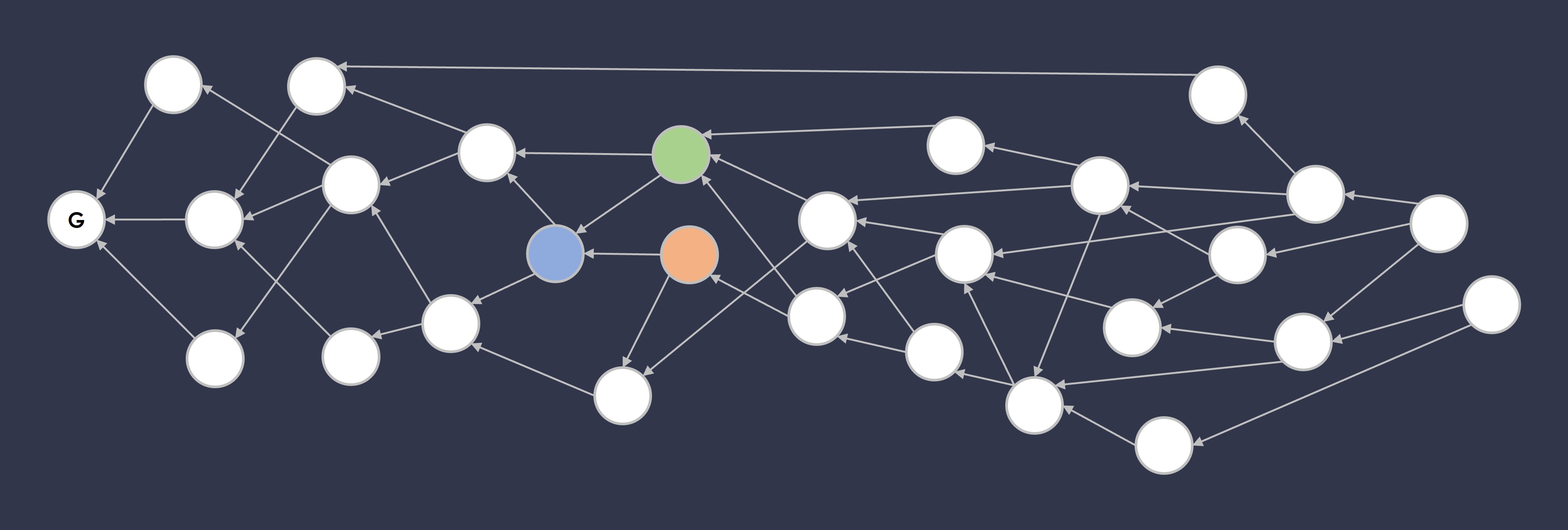
In the figure above, we can with 100% certainty say that the blue block definitely comes BEFORE the green and the orange blocks in ordering. Why? Since the green and orange blocks are pointing to the blue block, that means when the orange and green blocks were created, the blue block was already there, or else the orange and green blocks wouldn’t have known to point to it.
However, what about the ordering relationship between the green and orange blocks? There’s no certain answer to that question, depending on the type of ordering algorithm one uses, the order could be completely different.
Not only do we have one degree of freedom when it comes to ordering, there are also a myriad of choices that need to be made to ensure that the ordering algorithm is both fair and secure, in the sense that an honest majority of network participants cannot be somehow biased or attacked by a dishonest minority.
Let’s go through Taraxa’s block DAG’s ordering algorithm and see how we address these questions.
A Popularity Contest
In Taraxa’s block DAG topology, each block has backward pointers to not just a single parent block (like in a single-chain topology), but to all blocks at the frontier (edge) of the DAG that the block proposer has seen and believes to be valid. There are a lot of concepts here, let’s unpack them one by one.
What is a frontier? In a block DAG (or any DAG data structure), the frontier is simply the newest set of blocks that have no other blocks pointing back to them yet.
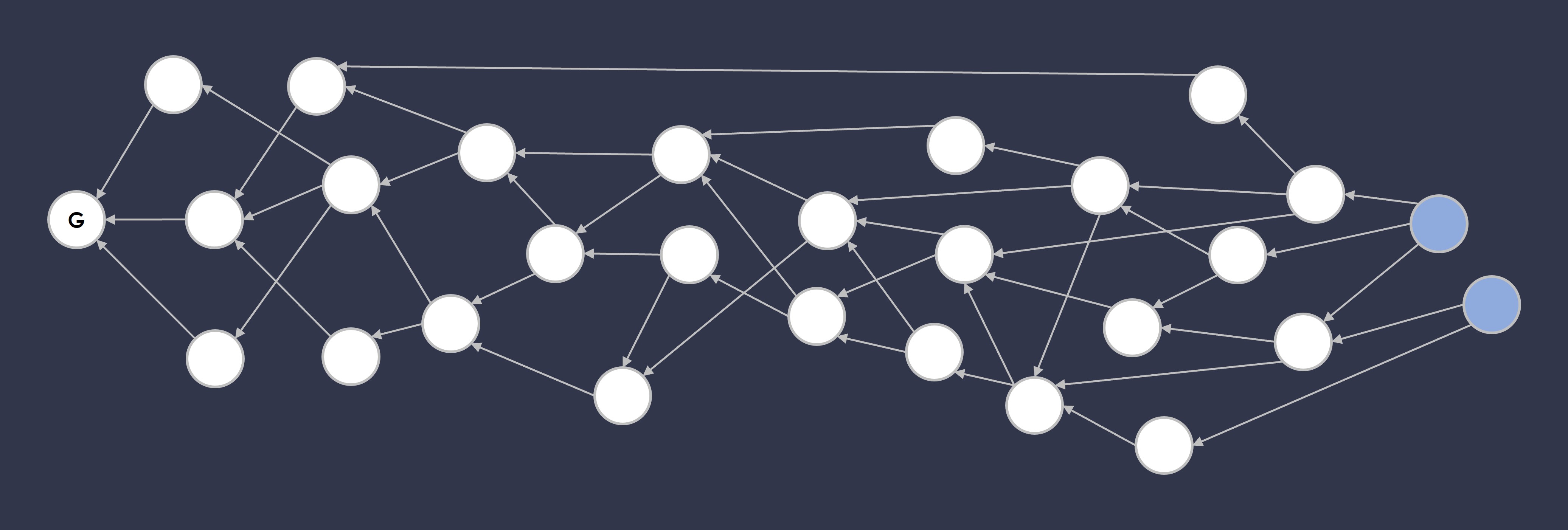
In the figure above, the blue blocks are the "frontier" blocks, while the rest of the blocks are not. The frontier is interesting because these blocks are the starting point from which the block proposer should be building on top of — in the sense that the next new blocks should be referring to these blocks. However, because every node sees very different network propagation delays when it comes to any given block, not every node will see the same frontier (or the same block DAG), so block proposers any given moment may be building their blocks based on different frontiers.
What is a pointer or a parent? A pointer is depicted as an arrow in the graph, it is a piece of data embedded inside a block that "points" or refers to another block, and in the case of Taraxa’s block DAG, they refer to set of parent blocks. Parent blocks are blocks that came before the blocks that are pointing at them — hence the term parent.
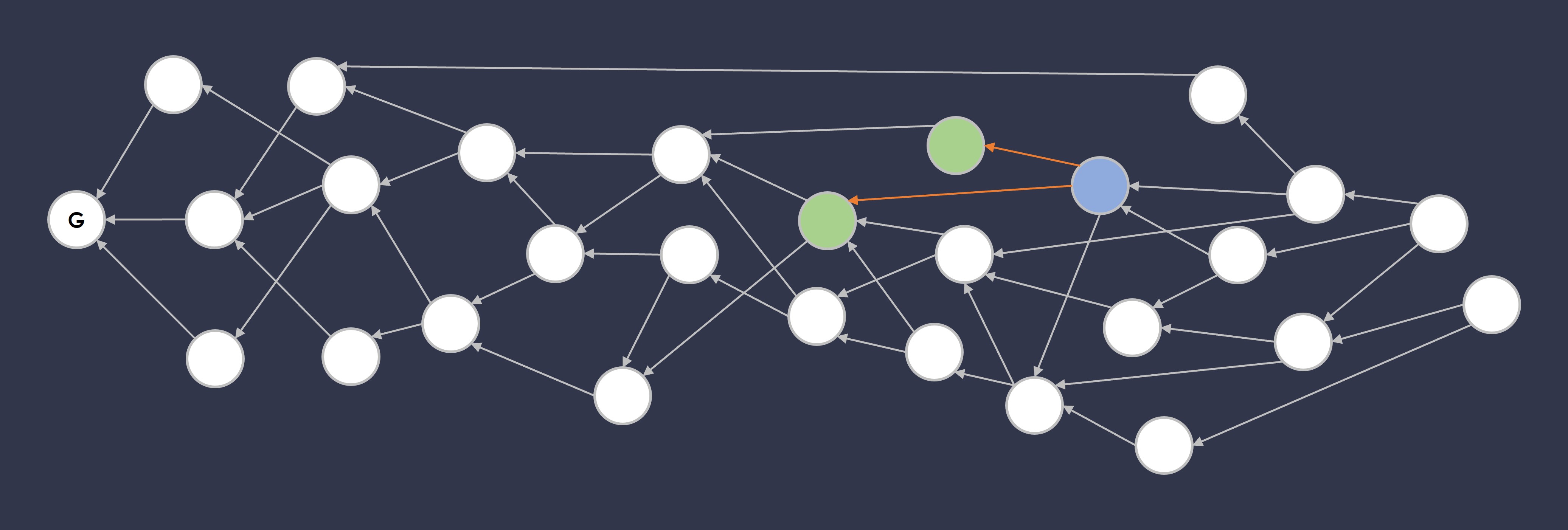
In the figure above, we see that the blue block has two pointers, pointing to two parents, represented by green blocks. This means that, at the time that the blue block was created by the block proposer, the proposer is aware of two (2) blocks on the frontier of the block DAG, and deems these two blocks valid, hence the blue block it created points to both of them.
These pointers that connect the blocks is effectively a popularity contest — it is a contest to see which blocks have been pointed to by the greatest number of other blocks and were deemed valid. Furthermore, if the blocks that point to a particular block are themselves "popular" — have many other blocks pointing to them, that "popularity" is carried over to that particular block (the parent) as well.
Now let’s measure how popular each block is.
Weights — the Popularity Score
To measure each block’s popularity, we resort to the GHOST protocol, also proposed by Zohar and Sompolinsky. GHOST helps to calculate the weight (how "popular" each block is) of each block from the pointers embedded in the block DAG.
What is "weight"? If you turn the block DAG on its side, you can think of each child block and its descendants as hanging off from the parent and thus the weight of any block under GHOST is the weight of that block and all its descendants.
Weight represents the collective effort of all the people trying to build upon that block over time, even if that effort isn’t coordinated and is spread out into multiple descendants.
The GHOST protocol is very simple,
- Each block naturally has a weight of 1 by themselves
- Each block’s weight is equal to its own weight (1) plus the weight of all blocks pointing to it
- Start at the frontier of the block DAG and measure backwards
Here’s an example.
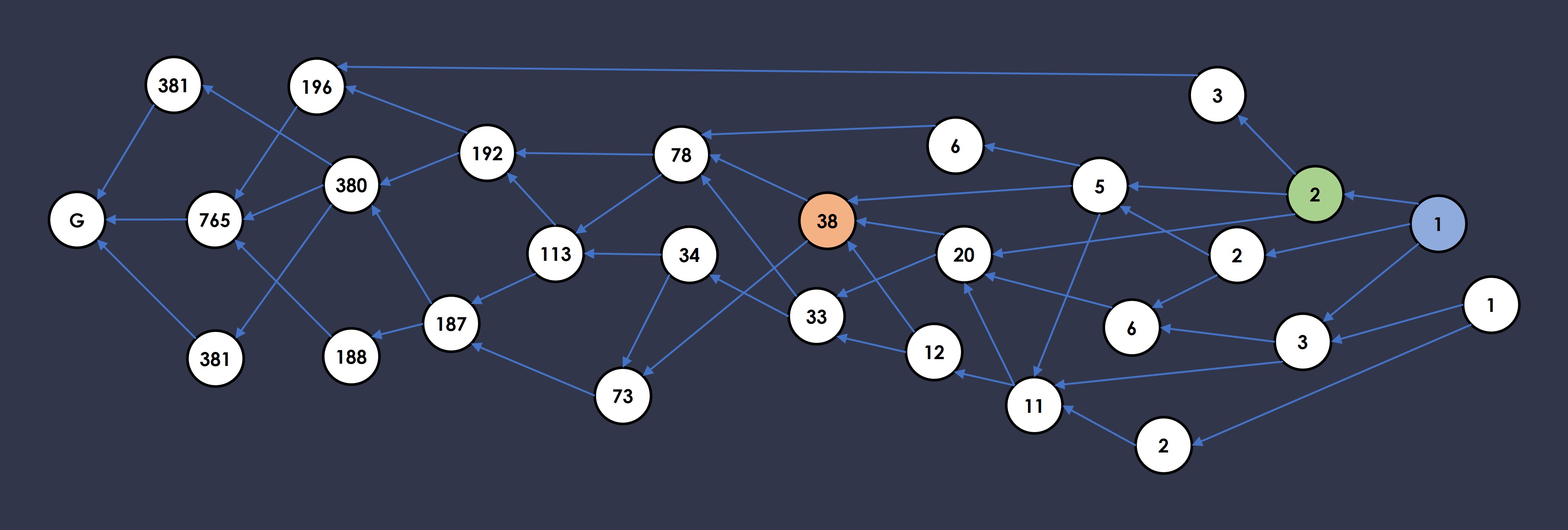
Working from the frontier backwards, we can assign each block with a weight. The blue block is at the block DAG’s frontier, with no blocks pointing at it, so it has its own weight of 1. The green block only has one single block pointing to it (the blue one), so we add the green block’s own weight (1) to the weight of the block pointing at it (1), and we get 2, which is the green block’s new weight. Reaching further in, the orange block has 3 blocks pointing to it, so its weight is the sum of the three blocks’ weights plus its own weight of 1: 5+20+12+1 = 38.
This looks great, can’t we now just order by weight? Well, not quite. There are some very nuanced problems with this simplistic strategy, let’s investigate them further.
Ways to Obfuscate Ordering
Let’s look at a simple example to understand why just using weights as the ordering mechanism is not sufficient.
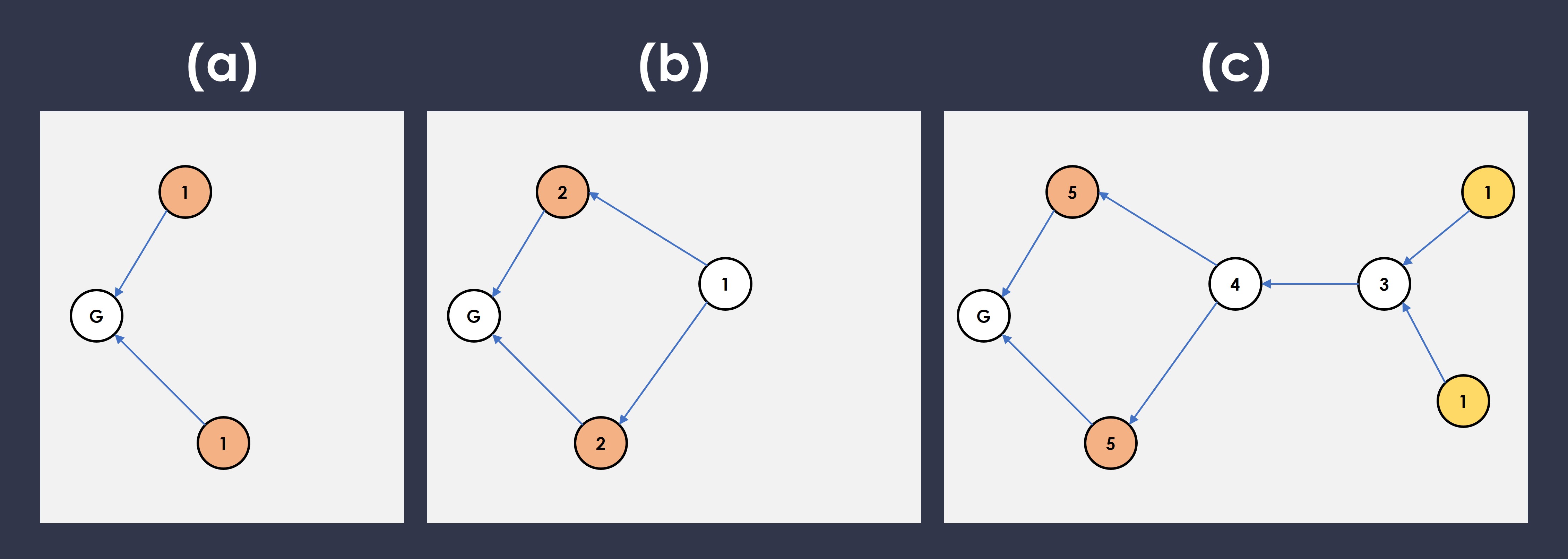
In the figure above, we start out with scenario (a).
- We see that there are two orange blocks both with weight of 1, so their order is ambiguous.
- Another block is created and it points to both previous blocks, but now both their weights are now 2, and still have ambiguous ordering.
- A few more blocks have added and not only have the problem with the orange blocks not gone away — they both still have the same weight, but now the situation is even worse — we have a new problem with the yellow blocks, which also have ambiguous ordering.
In the above example, we’re assuming everyone is acting honestly — and we still run into problems. What if you introduce a malicious player into the equation? That player could actively obfuscate ordering on block DAG. Let’s see the following example.
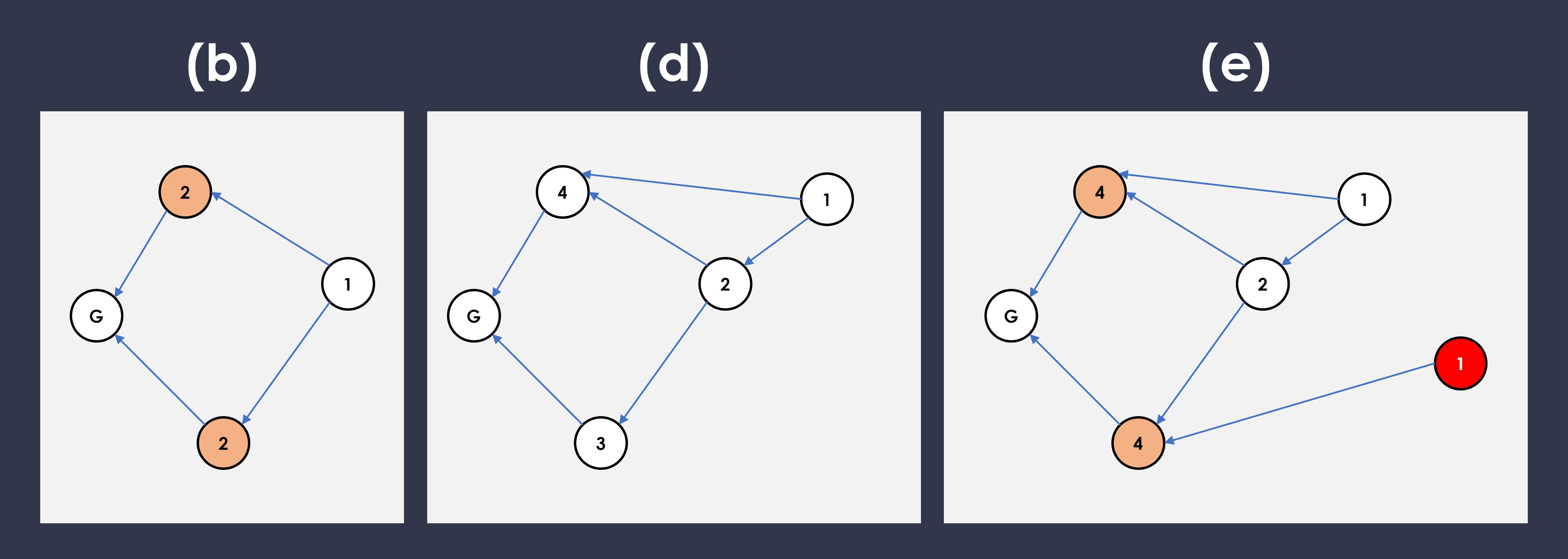
In this example, we start off at (b).
- We have 2 orange blocks with ambiguous order.
- Another block comes along and solves the the problem, and we now have non-ambiguous ordering. Hooray!
- But not so fast… a malicious player is actively seeking to keep the ordering ambiguous, and creates a block (red) which adds another point of weight, now we’ve returned to the same problem we had before, the two orange blocks are once again not well ordered.
Another implication of this type of attack is, not only can the malicious player keep the order ambiguous, he can also switch around the ordering back and forth to keep the network in a constant state of confusion.
Although these are very simple examples, but such problems could happen at a much larger scale in which entire clusters of blocks are being kept in ordering limbo.
So how do we resolve this problem? We introduce the concept of an anchor chain and the ghost pointer.
Anchor Chain — the Most Popular Pathway
The next step after we’ve calculated the weights is to identify an anchor chain in the block DAG. If the weight is a popularity score for each block, then the anchor chain is the most popular pathway through the block DAG. The blocks you would observe while traversing (walking) along the pathway are also guaranteed to be well-observed (very popular) by the network at large.
How do you construct the anchor chain? Simple! Just pick a starting point — or in the case of Taraxa, the starting point is the previous finalized period block (our article on finality coming soon) — and walk forward into its children, with each step selecting the block with the highest weight. Here’s an example,
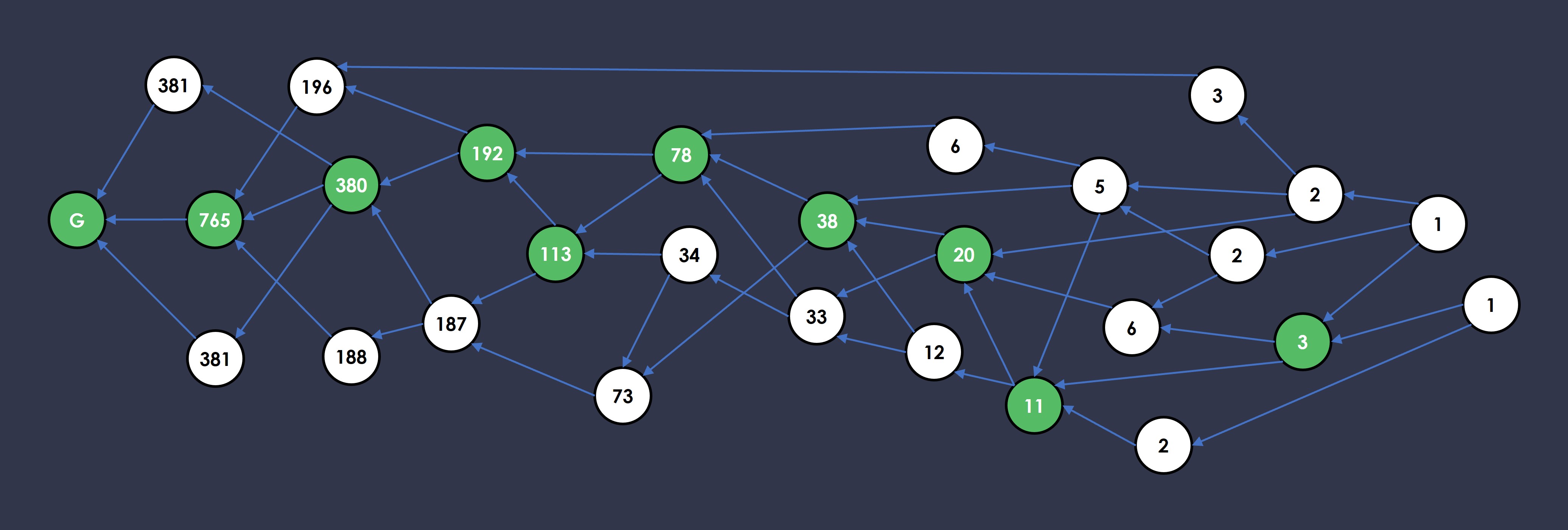
In the figure above, start at block G, walk forward, there are 3 blocks to choose from with weights (381, 765, 381), so the heaviest one is 765. You keep walking forward this way until you hit the end, constructing an anchor chain (in green).
The anchor chain does exactly that, it "anchors" the block DAG into a pathway based upon which we can now construct an ordering algorithm.
But this method of calculating the anchor chain takes into account every block being pointed to as having equal weight, which is also problematic as an attacker can still come in to constantly change the anchor chain (doesn’t converge very quickly). Therefore, we introduce the ghost pointer, to help the network converge more quickly onto a fixed anchor chain and thereby deterministic ordering.
Not all Pointers are Created Equal
To further prevent the network from being stuck in ordering limbo, we introduce a special pointer called the ghost pointer. The basic idea is that as each block is created, it points to all the blocks on the frontier that it sees and has validated to be legitimate, but one such block is special.
The special block is one that is the terminating block of an anchor chain, and each new block, in addition to acknowledging the existence of other legitimate blocks on the block DAG’s frontier, will point a ghost pointer at this terminating block. One important change here is that a block’s weight only take into account ghost-pointer blocks, not the acknowledgement pointers.
Parent blocks become only the block with the special ghost pointer pointing to it. Blocks in Taraxa’s block DAG point to only one parent. Other blocks are simply observed leaves, or "ancestors" — in Ethereum they’re referred to as "uncles" or "ommers". This could be either alluded to earlier on or maybe be very explicit and clear about this change in how many parents a block can have here.
This solves a fundamental issue of pointing to all blocks on the frontier as being a form of equivocating in the implicit voting process that a DAG graph represents.
Let’s run through a quick example,
- the thick arrows are the ghost pointers (counts weight)
- the thin dotted arrows are the acknowledgement pointers (no weight)
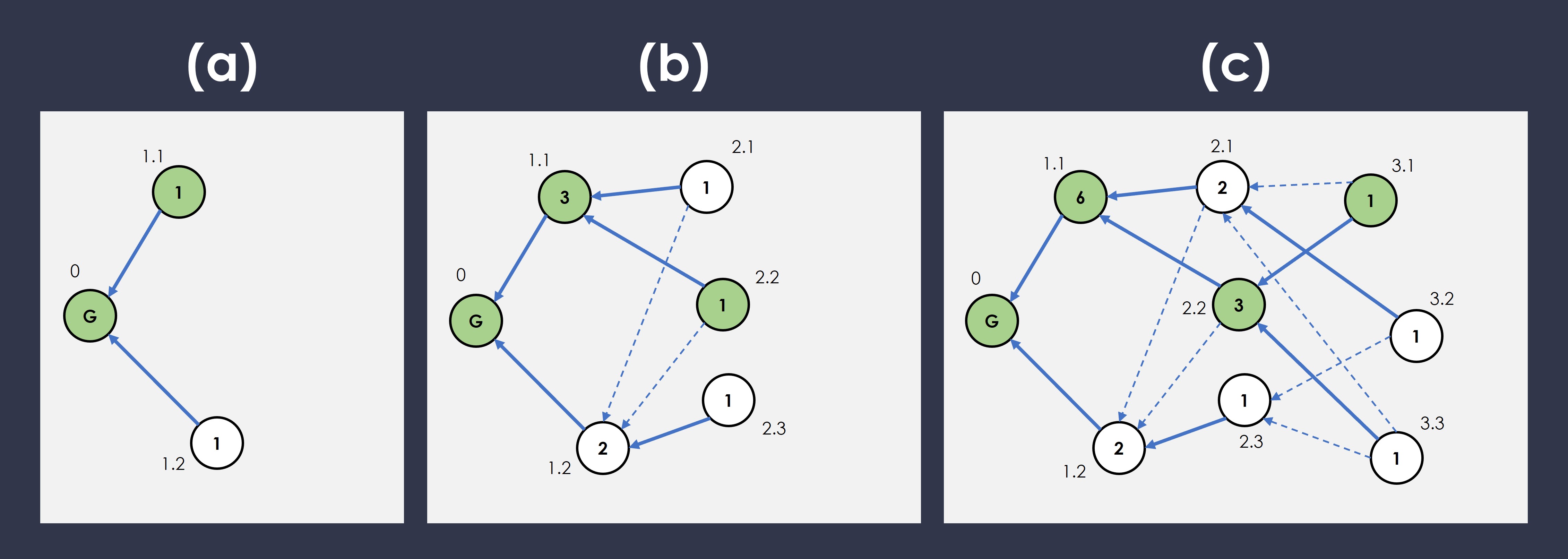
- Two blocks (1.1 and 1.2) pointing to the first genesis block (0), the thick line is the ghost pointer, since there’s only 1 block in existence they both point to it. Right now order is ambiguous but we an tie break using the lowest hash, let’s say (1.1) wins and is considered the candidate for the ghost pointer for future blocks.
- Three more blocks are added, but not all of these blocks see every block that was published due to network delay — i.e., certain blocks are seen faster by certain nodes due to, for example, being more closely connected with fewer network hops. Blocks (2.1) and (2.2) both have seen the previous two blocks (1.1 and 1.2), so they point to both of them and honestly identifies the (1.1)as the terminating block on the anchor chain, pointing their ghost pointers at it. The (2.3) however did not see the (1.1), so it only points to the (1.2) with a ghost pointer and nothing else. Note that, following our rule, the blocks’ weight have been updated but only taking into account children blocks who have pointed to it with ghost pointers.
- The next layer of blocks come in, block (3.1) has seen both (2.1) and (2.2), block (3.2) has seen (2.1) and (2.3), and (3.3) has seen all three (2.1, 2.2, and 2.3). Each block at the time of publication picks what they have seen as the terminating block on the anchor chain and points its ghost pointer at it, and we keep going.
The ghost pointer, in conjunction with the anchor chain, help to force the network to converge onto an anchor chain and stabilizing overall ordering. Next we describe how to finally order blocks based on the anchor chain.
Ordering via the Anchor Chain
Using the ghost pointer, let’s recalculate the weights on the block DAG example from before. Note that once again, only block pointing backwards with a ghost pointer can have its weight counted towards the parent block.
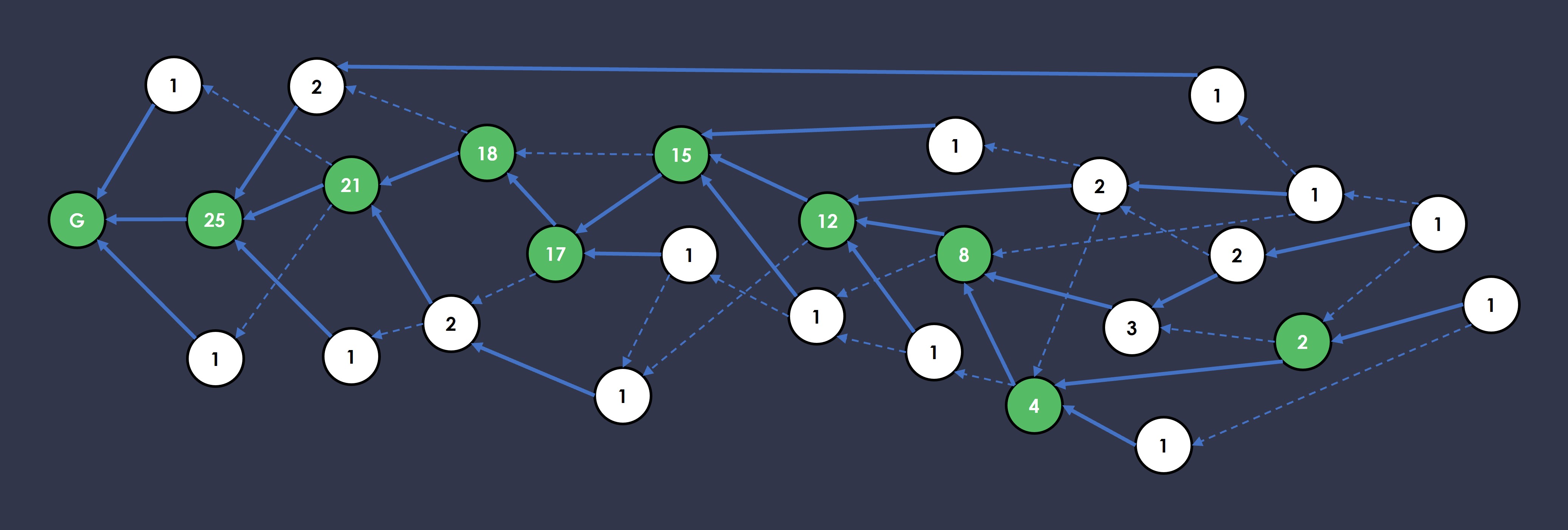
Once the anchor chain is mapped out, we construct epochs around each block (anchor block) on the anchor chain. An epoch is simply the blocks that are observable by the anchor block, or simply blocks that are either directly or indirectly pointed to by the anchor block. Think of them as the friends of the super popular anchor block.
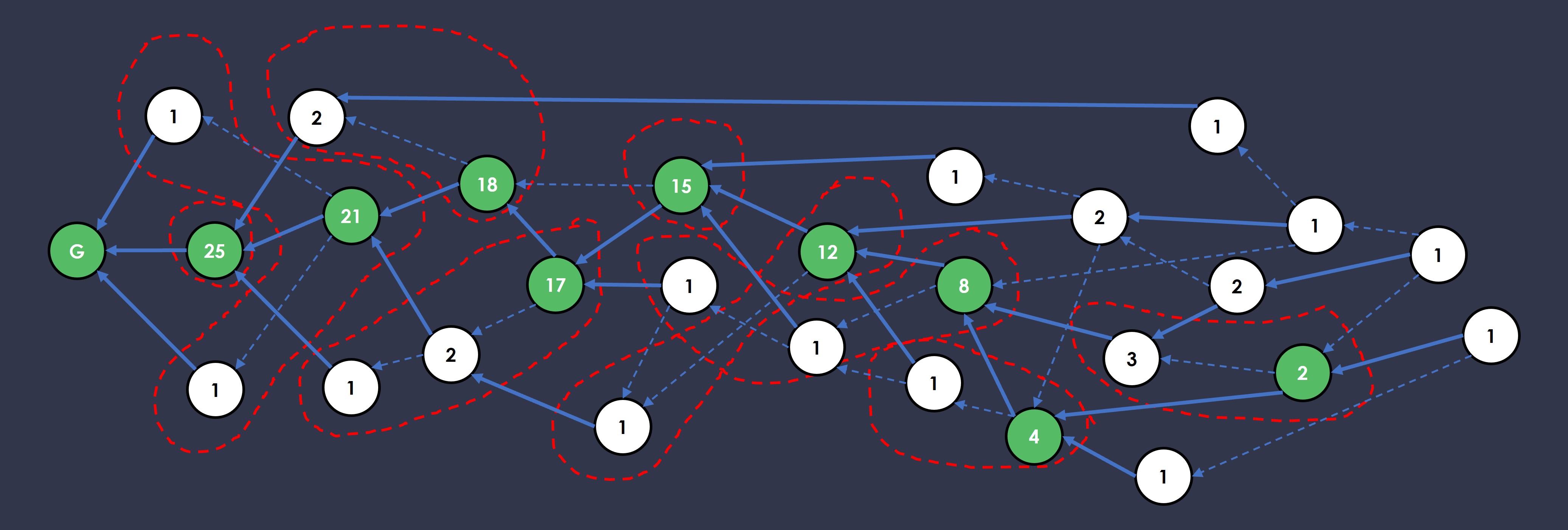
In the figure above, we use red dotted lines to draw out the epoch for each anchor block. The first anchor block with weight 25 unfortunately only has itself in the epoch. The next anchor block with weight 21 has an epoch consisting of itself and two other blocks it can observe, both with weights 1. The third anchor block has a weight of 18, with only one other block it can observe. The next one has a weight of 17, which has an epoch of 3 including a block with weight 1 which it directly observes, and another block 2 which it indirectly observes. We keep going until every anchor block’s epoch has been mapped out.
Now we are ready to order the blocks! The blocks are ordered first by epoch from oldest to newest (left to right). Within each epoch, the order is determined by which blocks came first by looking at who’s pointing to whom, and using the weight, or if that fails, the block hash as tie breaker for blocks that are the same distance away from the anchor block.
Looking at the epoch figure, G is the first one (1). We move into the next epoch which only has one block, so that block with weight 25 is the second block (2). Moving onto the next epoch, the two blocks with weight 1 come before the anchor block with weight 21 (since they are pointed to by the block with weight 21), and we can say we use a lowest hash tie breaker to determine (3) and (4), then the block with 21 is the fifth block (5). We keep going until all the blocks within all the epochs are ordered.
See below, numbers inside each block represents order, not weight.
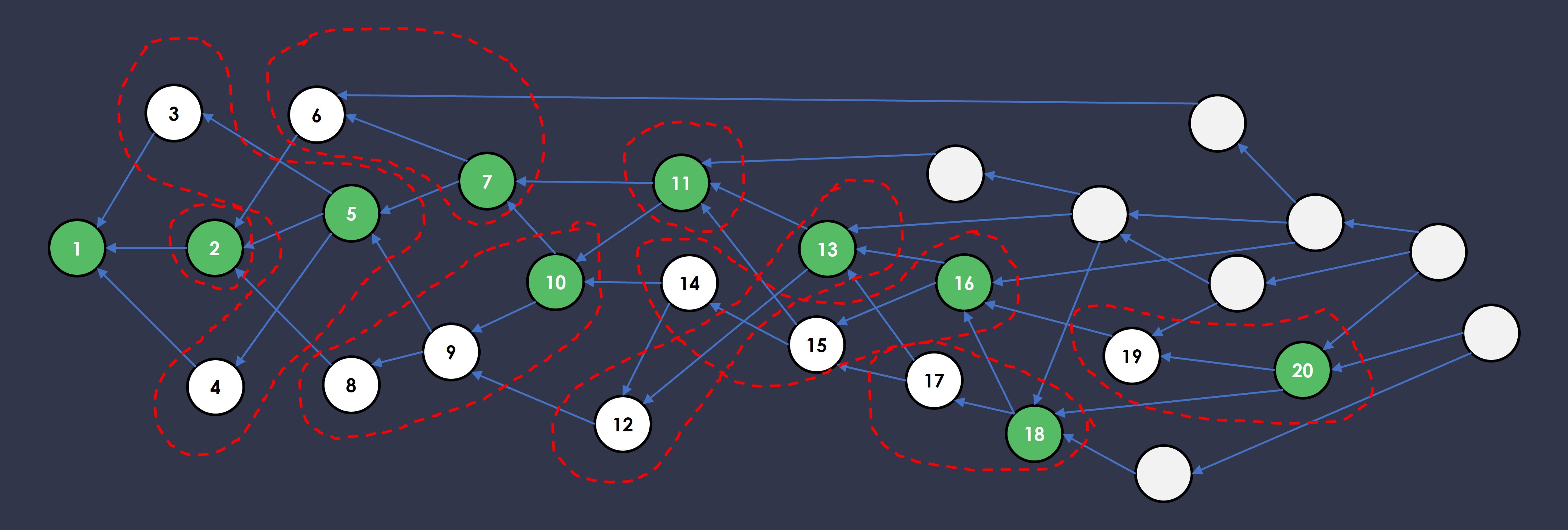
We’re done!
But are we really done? What about those blocks that weren’t ordered?
There are always blocks near the block DAG’s frontier that aren’t included as part of the anchor chain’s epochs. But don’t worry, they’ll be eventually included as more blocks are added to the frontier.
Doesn’t the anchor chain (and therefore ordering) change over time?
Yes! There is a risk of re-ordering within the block DAG. This risk falls off exponentially over time but is never truly eliminated. This is why Taraxa has implemented a rapid finalization process that introduces true finality into the block DAG with zero risk of re-ordering, giving DApps the peace of mind often necessary to move forward.
Stay tuned.
